解析延拓与发散级数
这张图展示的是一个 非常著名但也最容易被误解的数学公式:
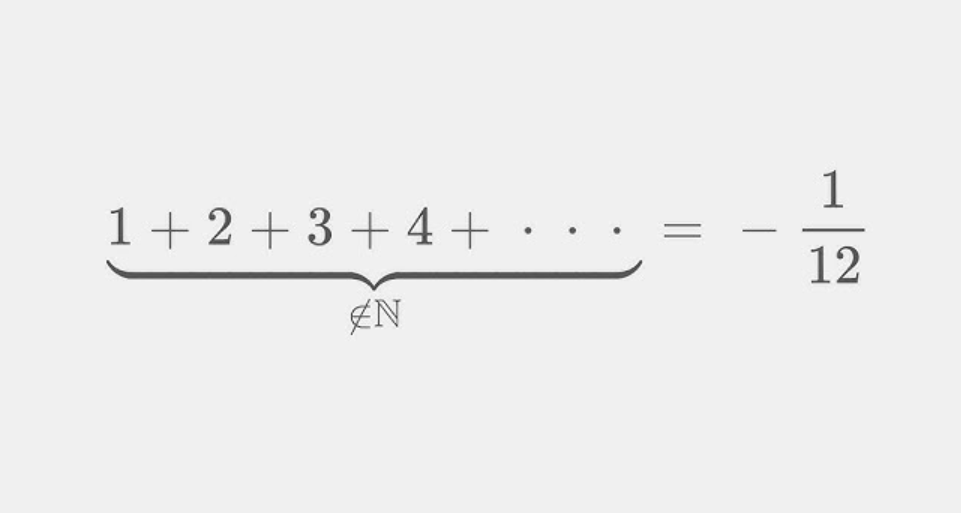
它不是在说“所有正整数加起来真的等于 -1/12”!
真实的普通意义上的无穷级数:
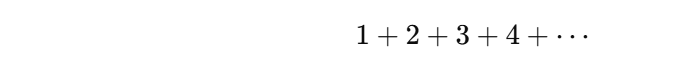
是 发散的,也就是说——它并没有一个有限的和,更不可能是负数。
✔ 那么它为什么会等于 −1/12-1/12−1/12?
这是在 高等数学 中使用的一种叫作 解析延拓(analytic continuation) 的技术。
它来自 黎曼ζ函数(Riemann zeta function):
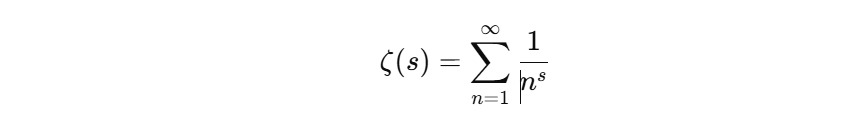
s=−1 时,原本的级数变成:
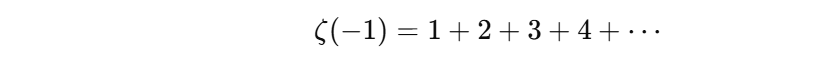
所以:
✨ -1/12 不是普通求和的结果,而是 ζ 函数在 s = -1 处的解析延拓值。
✔ 那这个值有什么用?
非常多,尤其是在 物理学 里:
在弦理论里:
弦的一阶能量振动计算会出现:
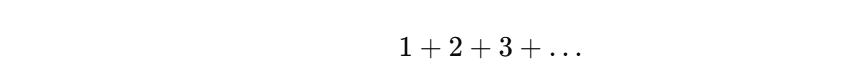
为了得到物理可测量的值,需要通过 ζ 函数正则化,使其等于:



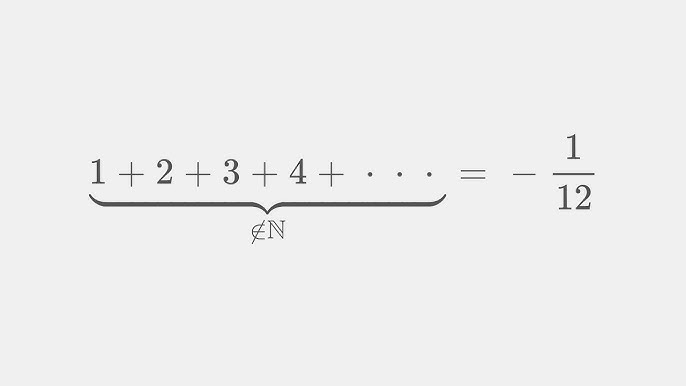












Comment